LV.AMO.2024.8.5 lv
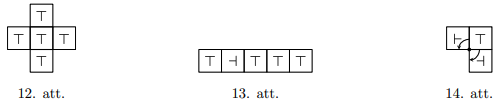
Dotas piecas smagas kastes un tās izkārtotas, kā tas redzams 12. att. Šīs kastes var pārvietot tikai pagriežot par 90 grādiem ap kādu no kastes stūriem. Kastes nav iespējams pārvietot citām kastēm virsū. Pēc vairākiem šādiem pārvietojumiem šīs kastes tika izkārtotas, kā tas redzams 13. att. Kuras no šīm kastēm varēja sākotnēji atrasties 12. att. izkārtojuma centrā? Piemēru, kā kasti var pārvietot ap vienu stūri divos dažādos veidos skatīt 14. att.
Atrisinājums
Pamatosim, ka sākotnējā izkārtojumā centrā varēja atrasties tikai ceturtā kaste. Iztēlosimies, ka kastes pilnībā atrodas uz šaha galdiņa izkārtojuma flīzēm, kuru izmēri sakrīt ar katras kastes izmēriem. Tādā gadījumā varam uzskatīt, ka sākotnējā izkārtojumā centrālā kaste atrodas uz baltas flīzes, bet apkārtējās uz melnām flīzēm. Katru reizi, kad pārbīdām kasti, tā atradīsies uz pretējas krāsas flīzes. Varam ievērot, ka rezultējošajā izkārtojumā četras no kastēm tika pārbīdītas pāra skaitu reižu, jo to simboli atrodas tādā pašā orientācijā kā sākumā. Tas nozīmē, ka šīs kastes atrodas uz tādām pašām krāsu flīzēm kā sākotnējā izkārtojumā. Tā kā 3., 4. un 5. kaste atrodas viena otrai blakus, tad vismaz viena no tām atrodas uz baltas flīzes. Varētu gadīties, ka gan 3., gan 5. kastes atrodas uz baltas flīzes, bet tas nav iespējams, jo sākotnēji tikai viena kaste atradās uz baltas flizes, bet 3., 4. un 5. kaste atrodas uz flīzes, kuras krāsa sakrīt ar sākotnējā izkārtojuma flīzes krāsu. Tātad 4. kaste atrodas uz baltas flīzes un tās flīzes krāsa nav mainījusies. Secinām, ka šī ir tieši tā kaste, kas sākotnēji atradās centrā.
Lai iegūtu prasīto sakārtojumu no sākotnējā, tad vispirms kasti, kas atrodas virspusē, pārvietojam pa kreisi līdz tā atrodas vienā rindā ar vidējām kastēm, un visbeidzot apakšējo kasti arī pārbīdām pa kreisi līdz tā atrodas vienā rindā ar visām kastēm. Šādi centra kaste ir ceturtā pēc kārtas, kā tas prasīts.