LV.AMO.2024.8.4 lv
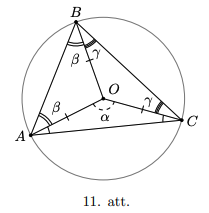
Uz riņk̦a līnijas ar centru \(O\) ir atlikti punkti \(A, B\) un \(C\) tā, lai punkts \(O\) atrastos trijstūrī \(ABC\). Pie tam zināms, ka \(\sphericalangle AOC=\alpha\), bet \(\sphericalangle OAB=\beta\). Izteikt leņķi \(\sphericalangle BCO\) ar \(\alpha\) un \(\beta\)!
Atrisinājums
Ievērosim, ka trijstūris \(AOC\) ir vienādsānu, jo \(AO=CO\) kā riņka līnijas rādiusi. Ņemot vērā, ka vienādsānu trijstūrim pamata leņk̦i ir vienādi un ka trijstūrī leņk̦u summa ir \(180^{\circ}\), iegūstam, ka
\[\sphericalangle CAO=\sphericalangle OCA=\frac{180^{\circ}-\alpha}{2} = 90^{\circ}-\frac{\alpha}{2}\]
Līdzīgi varam spriest arı̄ par vienādsānu trijstūri \(ABO\) (\(AO=BO\) kā riņka līnijas rādiusi) un iegūt, ka \(\sphericalangle ABO=\beta\). Apzīmēsim \(\sphericalangle BCO\) ar \(\gamma\). Tā kā trijstūris \(BOC\) ir vienādsānu (\(BO\) un \(CO\) ir vienādi kā riņk̦a līnijas rādiusi), tad \(\sphericalangle BCO=\sphericalangle OBC=\gamma\). Ņemot vērā, ka trijstūra \(ABC\) iekšējā leņķu summa ir \(180^{\circ}\), iegūstam (skatīt 11. att.), ka\[90^{\circ}-\frac{\alpha}{2}+90^{\circ}-\frac{\alpha}{2}+\beta+\beta+\gamma+\gamma=180^{\circ}\]
jeb\[2 \gamma=180^{\circ}-180^{\circ}+\alpha-2 \beta \Longrightarrow \gamma=\frac{a}{2}-\beta\]
Secinām, ka \(\sphericalangle OBC=\frac{\alpha}{2}-\beta\).