Atrisinājums

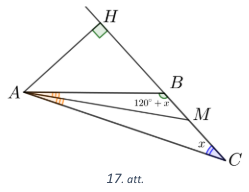
Apzīmējam trijstūra virsotnes ar \(A, B, C\) un pieņemsim, ka \(\sphericalangle B = \sphericalangle C + 120^{\circ}\) (skat. 17. att.). Apzīmējam \(\sphericalangle C = x\), tad \(\sphericalangle B = 120^{\circ} + x\) un \(\sphericalangle A = 180^{\circ} - \sphericalangle B − \sphericalangle C = 60^{\circ} − 2x\).

No virsotnes \(A\) novelkam augstumu \(AH\) un bisektrisi \(AM\). Tā kā \(AM\) ir bisektrise, tad \(\sphericalangle MAC = \frac{1}{2}\sphericalangle A = 30^{\circ} - x\). Leņķis \(\sphericalangle AMH\) ir trijstūra \(MCA\) ārējais leņķis, tātad \(\sphericalangle AMH = \sphericalangle MAC + \sphericalangle MCA = 30^{\circ} − x + x = 30^{\circ}\). Tas nozīmē, ka taisnleņķa trijstūrī \(AHM\) katete \(AH\) atrodas pret \(30^{\circ}\) leņķi, tātad tā ir vienāda ar pusi no hipotenūzas \(AM\) jeb \(AM = 2AH\).