LV.AMO.2023.8.3 lv
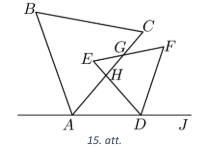
Divi vienādmalu trijstūri novietoti plaknē kā parādīts 15. att. Zināms, ka \(\sphericalangle CAD = \alpha\) un \(\sphericalangle FDJ = \beta\). Izsaki leņķi \(CGF\) ar \(\alpha\) un \(\beta\).
Atrisinājums
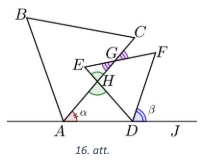
Tā kā regulāra trijstūra visi leņķi ir \(60^{\circ}\), tad \(\sphericalangle HDA = 180^{\circ} − \sphericalangle FDJ - \sphericalangle EDF = 180^{\circ} - \beta - 60^{\circ} = 120^{\circ} - \beta\) (skat. 16. att.). Izmantojot krustleņķu īpašību un trijstūra iekšējo leņķu summu, iegūstam:
- \(\sphericalangle EHG = \sphericalangle AHD = 180^{\circ} − \alpha − (120^{\circ} − \beta) = 60^{\circ} − \alpha + \beta\);
- \(\sphericalangle CGF = \sphericalangle EGH = 180^{\circ} − 60^{\circ} − (60^{\circ} − \alpha + \beta) = 60^{\circ} + \alpha - \beta\).
Tātad \(\sphericalangle CGF = \sphericalangle EGH = 60^{\circ} + \alpha − \beta\).