Atrisinājums

Apzīmēsim \(AD = a\) un \(AB = b\). Tādā gadījumā \(BD = \sqrt{a^2 + b^2}\), no kā iegūstam, ka \(S_{BDEF} = BD^2 = a^2 + b^2\).

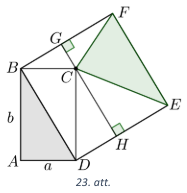
Caur punktu \(C\) novelkam nogriezni \(GH\), kas ir paralēls kvadrāta malai \(BD\) (skat. 23. att.). Taisnstūra diagonāle \(BD\) sadala taisnstūra \(ABCD\) laukumu divos vienādos trijstūros \(ABD\) un \(BCD\), kuru laukumi ir \(S_{ABD} = S_{BCD} = \frac{ab}{2}\).

Tā kā trijstūra \(BCD\) pamats ir taisnstūra \(BDHG\) mala \(BD\), bet trijstūra augstuma garums ir vienāds ar taisnstūra malas \(BG\) garumu, tad \(S_{BDHG} = 2S_{BCD} = ab\). Līdzīgi iegūstam, ka \(S_{CEF} = \frac{1}{2}S_{EFGH}\). Līdz ar to

\[S_{CEF} = \frac{1}{2}S_{EFGH} = \frac{S_{BDEF} - S_{BDHG}}{2} = \frac{a^2 + b^2 - ab}{2} = \frac{(a-b)^2 + ab}{2} \geq \frac{ab}{2} = S_{ABD}.\]