Atrisinājums

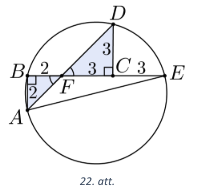
Pagarinām nogriezni \(BC\) līdz tas krusto riņķa līniju punktā \(E\) (skat. 22. att.). Tādā gadījumā \(AE\) būs riņķa līnijas diametrs, jo uz tā balstās taisnais leņķis \(\sphericalangle ABE\). Papildus novelkam nogriezni \(AD\) un tā krustpunktu ar \(BC\) apzīmēsim ar \(F\). Trijstūri \(\triangle ABF\) un \(\triangle FCD\) ir līdzīgi pēc pazīmes \(\ell\ell\), jo abi ir taisnleņķa un \(\sphericalangle AFB = \sphericalangle CFD\). No šī izriet, ka

\[\frac{AB}{BF} = \frac{CD}{CF}\;\;\Rightarrow\;\; \frac{2}{BF} = \frac{3}{FC} \;\;\Rightarrow\;\; \frac{2}{BF} = \frac{3}{5 - BF} \;\;\Rightarrow\;\; BF = 2, CF=3.\]

Tātad \(\triangle CDF\) ir vienādsānu taisnleņķa trijstūris, jo \(CF = CD = 3\). Tātad \(\sphericalangle CDF = 45^{\circ}\). Tā kā ievilktais leņķis ∢𝐴𝐷𝐸 balstās uz diametru \(AE\), tad \(\sphericalangle ADE = 90^{\circ}\). No kā izriet, ka

\[\sphericalangle CDE = \sphericalangle ADE − \sphericalangle CDF = 90^{\circ} − 45^{\circ} = 45^{\circ}.\]

Tātad arī \(\triangle CDE\) ir taisnleņķa vienādsānu trijstūris, kurā \(CD = CE = 3\). Tātad \(BE = BF + CF + CE = 8\) un diametrs \(AE = \sqrt{8^2 + 2^2} = \sqrt{68} = 2\sqrt{17}\). Līdz ar to riņķa laukums \(S = \frac{\pi{}AE^2}{4} = 17\pi\).