LV.AMO.2022B.9.4 en lv
Vai pa apli var uzrakstīt skaitļus
(A) 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13;
(B) 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14;
tā, lai katri divi blakus esoši skaitļi atšķirtos par \(3\); \(4\) vai \(5\)?
Atrisinājums
(A) Pamatosim, ka prasītais nav iespējams.
Ievērosim, ka skaitļi \(1\); \(2\); \(3\); \(11\); \(12\) un \(13\) nevar būt uzrakstīti blakus viens otram, jo katru divu skaitļu starpība nav \(3\); \(4\) vai \(5\). Tātad tos jāraksta, izlaižot vienu pozīciju, tādējādi rodas tikai divas blakus vietas, kurās nav ierakstīti skaitļi (skat. 10.att.).
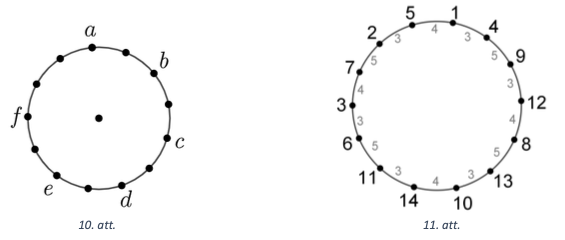
Skaitli 4 var rakstīt blakus tikai skaitlim \(1\), jo to starpība ir \(3\), bet to nevar rakstīt blakus pārējiem jau uzrakstītajiem skaitļiem \(2\); \(3\); \(11\); \(12\) vai \(13\). Tātad skaitli \(4\) jāraksta vienā no divām blakus esošajām brīvajām vietām.
Skaitli \(10\) var rakstīt blakus tikai skaitlim 13, bet to nevar rakstīt blakus pārējiem pa apli uzrakstītajiem skaitļiem \(1\); \(2\); \(3\); \(11\) vai \(12\). Tātad skaitli 10 jāraksta vienā no divām blakus esošajām brīvajām vietām. No tā izriet, ka skaitļus 4 un 10 jāraksta blakus, bet rodas pretruna ar uzdevuma nosacījumiem, jo to starpība ir \(6\). Tātad dotos skaitļus nevar uzrakstīt tā, lai katri divi blakus esoši skaitļi atšķirtos par \(3\); \(4\) vai \(5\).
(B) Jā, var, piemēram, skat. 11. att., kur rinķa iekšpusē ierakstīts, par cik atšķiras skaitļi.