LV.AMO.2022B.9.3 en lv
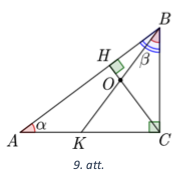
Taisnleņķa trijstūrī \(ACB\) (\(\sphericalangle C = 90^{\circ}\)) novilkts augstums \(CH\). Uz malas \(AC\) atlikts punkts \(K\) tā, ka \(\sphericalangle CBK = \sphericalangle BAC\). Pierādīt, ka taisne \(CH\) dala nogriezni \(BK\) divās vienādās daļās!
Atrisinājums
Apzīmējam \(CH\) un \(KB\) krustpunktu ar \(O\) un \(\sphericalangle CBK=\sphericalangle BAC=\alpha\), \(\sphericalangle ABC=\beta\) (skat. 9.att.). No trijstūra \(ABC\) iegūstam, ka \(\sphericalangle BAC=180^{\circ}-\sphericalangle ACB-\sphericalangle ABC\) jeb \(\alpha=90^{\circ}-\beta\). No trijstūra \(BHC\) iegūstam, ka \(\sphericalangle HCB=180^{\circ}-\sphericalangle CHB-\sphericalangle HBC=90^{\circ}-\beta=\alpha\), tātad trijstūris \(COB\) ir vienādsānu trijstūris, jo divi tā leņķi ir vienādi \(\sphericalangle OBC=\sphericalangle OCB=\alpha\). No tā izriet, ka \(BO = OC\) kā vienādsānu trijstūra sānu malas.
No trijstūra \(KCB\) iegūstam, ka \(\sphericalangle BKC=180^{\circ}-\sphericalangle KCB-\sphericalangle KBC = 90^{\circ}-\alpha=\beta\). Ievērojam, ka \(\sphericalangle ACH=\sphericalangle ACB-\sphericalangle HCB=90^{\circ}-\alpha=\beta\). Tātad trijstūris \(KOC\) ir vienādsānu, jo divi tā leņķi ir vienādi \(\sphericalangle OKC=\sphericalangle KCO = \beta\), un tā sānu malas ir vienādas \(CO=OK\).
No vienādībām \(BO=OC\) un \(CO=OK\) iegūstam, ka \(BO=OK\), tātad \(CH\) dala nogriezni \(BK\) divās vienādās daļās