LV.AMO.2022B.8.3 en lv
Trijstūrī \(ABC\) uz malas \(BC\) atlikts tāds punkts \(D\), ka \(AD = BD\) un \(AB = DC = AC\). Aprēķināt trijstūra \(ABC\) leņķus!
Atrisinājums
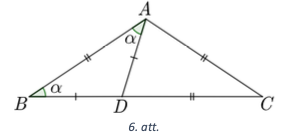
Tā kā \(AD=BD\), tad trijstūris \(ABD\) ir vienādsānu trijstūris ar pamatu \(AB\) un tā pamata pielenķi ir vienādi, tātad \(\sphericalangle ABD=\sphericalangle BAD=\alpha\) (skat. 6. att.).
No trijstūra \(ABD\) iegūstam, ka \(\sphericalangle ADB=180^{\circ}-\alpha-\alpha=180^{\circ}-2 \alpha\).
Ievērojam, ka \(\sphericalangle ADC=180^{\circ} - \sphericalangle ADB=180^{\circ}-\left(180^{\circ}-2 \alpha\right)=2 \alpha\) kā blakusleņki. Tā kā \(AC=DC\), tad arī trijstūris \(ACD\) ir vienādsānu un tā pamata pieleņki ir vienādi, tātad \(\sphericalangle DAC=\sphericalangle ADC = 2\alpha\).
Tā kā \(AB=AC\), tad arī trijstūris \(ABC\) ir vienādsānu un tā pamata pieleņķi ir vienādi, tātad \(\sphericalangle ABC=\sphericalangle ACB=\alpha\). No trijstūra \(ACD\) iegūstam, ka
\[\sphericalangle ADC+\sphericalangle DAC+\sphericalangle ACD = 2 \alpha+2 \alpha+\alpha=180^{\circ}\]
Atrisinot vienādojumu \(5 \alpha=180^{\circ}\), iegūstam, ka \(\alpha=36^{\circ}\). Aprēkinām trijstūra \(ABC\) leņķu vērtības:\[\begin{aligned} & \circ \quad \sphericalangle ABC = \sphericalangle ACB = \alpha=36^{\circ};\\ & \circ \quad \sphericalangle BAC = \sphericalangle BAD + \sphericalangle DAC = \alpha+2 \alpha=108^{\circ}. \end{aligned}\]