Atrisinājums

Apzīmēsim \(AB\) viduspunktu ar \(M\) un novilksim perpendikulus \(MP\) un \(MT\) attiecīgi pret malām \(AC\) un \(BC\). Augstuma pamatus, kas vilkti no virsotnēm \(A\) un \(B\), apzīmēsim attiecīgi ar \(Q\) un \(N\). Tā kā \(MT \| AQ\), jo \(MT \perp BC\) un \(AQ \perp BC\), tad \(M T\) ir trijstūra \(A Q B\) viduslīnija, tātad \(M T=\frac{1}{2} A Q=\frac{1}{2}\). Līdzīgi iegūstam, ka \(M P=\frac{1}{2} B N=\frac{\sqrt{3}}{2}\).

Ievērojam, ka taisnleņķa trijstūrī \(MTC\) izpildās, ka \(\sin \sphericalangle MCT=\frac{M T}{M C}=\frac{1}{2}\), tātad \(\sphericalangle M C T=30^{\circ}\). Līdzīgi iegūstam, ka taisnleņka trijstūrī \(MPC\) izpildās, ka \(\sin \sphericalangle M C P=\frac{M P}{M C}=\frac{\sqrt{3}}{2}\), tātad \(\sphericalangle M C P=60^{\circ}\).

Aplūkojam iespējamās \(\sphericalangle MCB\) vērtības:

• ja \(T\) atrodas uz \(BC\), tad \(\sphericalangle M C B=30^{\circ}\);
• ja \(T\) atrodas uz \(BC\) pagarinājuma, tad \(\sphericalangle M C B=150^{\circ}\).

Tā kā \(\sphericalangle ACB=\sphericalangle MCA+\sphericalangle MCB\), gadījums, ka \(\sphericalangle MCB=150^{\circ}\), nav iespējams, jo tad pie jebkuras \(\sphericalangle M C B\) vērtības \(\sphericalangle A C B\) būs vienāds vai lielāks nekā \(180^{\circ}\). No tā izriet, ka \(\sphericalangle MCB=30^{\circ}\).

Līdzīgi aplūkojam iespējamās \(\sphericalangle MCA\) un \(\sphericalangle ACB\) vērtības:

• ja \(P\) atrodas \(AC\), tad \(\sphericalangle MCA = 60^{\circ}\) un \(\sphericalangle ACB = 90^{\circ}\),
• ja \(P\) atrodas uz \(AC\) pagarinājuma, tad \(\sphericalangle MCA = 120^{\circ}\) un \(\sphericalangle A C B=150^{\circ}\).

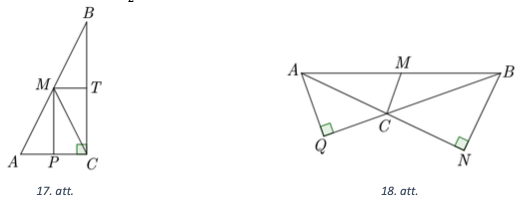
Ja \(\sphericalangle ACB=90^{\circ}\) (skat. 17. att.), tad augstumi no virsotnēm \(A\) un \(B\) sakrīt ar katetēm \(AC\) un \(BC\), tātad

\[S_{ABC}=\frac{AC \cdot BC}{2}=\frac{1 \cdot \sqrt{3}}{2}=\frac{\sqrt{3}}{2}.\]

Ja \(\sphericalangle ACB=150^{\circ}\) (skat. 18. att.), aplūkojam taisnleņķa trijstūri \(AQC\), kurā \(\sphericalangle A C Q=30^{\circ}\), tātad \(\frac{A Q}{A C}=\sin \sphericalangle ACQ=\frac{1}{2}\). No tā izriet, ka \(A C=2 \cdot A Q=2\) un

\[S_{ABC}=\frac{AC \cdot BN}{2}=2 \cdot \frac{\sqrt{3}}{2}=\sqrt{3}.\]

Tātad trijstūra laukums var būt \(\frac{\sqrt{3}}{2}\) vai \(\sqrt{3}\).