LV.AMO.2022B.11.5 en lv
Mākslas muzeja plānojums ir taisnstūris ar izmēriem \(m \times n\) (\(m \geq 2\), \(n \geq 2\)) rūtiņas, kur viena rūtiņa atbilst vienai muzeja telpai. Muzeja vadītājs vēlas izveidot apmeklētāju maršrutu, kuram izpildās šādas īpašības:
- maršruts sākas kādā no rūtiņām (telpām), kas atrodas pie taisnstūra malas;
- apmeklētājs no vienas rūtiņas (telpas) var pāriet uz citu rūtiņu (telpu), ja tām ir kopīga mala;
- apmeklētājs maršruta laikā apmeklē katru rūtiņu (telpu) tieši vienu reizi;
- maršruts beidzas rūtiņā (telpā), kas atrodas pie taisnstūra malas blakus maršruta sākuma rūtiņai (telpai).
Kādām \(m\) un \(n\) vērtībām muzeja vadītājs var izveidot šādu maršrutu?
Atrisinājums
Muzeja vadītājs var izveidot aprakstīto maršrutu visām \(m;n \geq 2\) vērtībām, kurām vismaz viens no \(m\) vai \(n\) dalās ar 2. Aplūkojam trīs gadījumus.
-
Ja \(m=2\) un \(n \geq 2\), pagriezīsim taisnstūri tā, lai \(m=2\) būtu rindu skaits. Tātad maršruta pirmā daļa ved no apakšējā kreisā stūra uz apakšējo labo stūri (visa apakšējā rinda), tālāk uz augšējo labo stūri un pēc tam augšējo kreiso stūri (visa augšējā rinda). Redzams, ka maršruts apmierina uzdevuma nosacijumus.
-
Ja \(m>2\) dalās ar \(2\) un \(n>2\), pagriezīsim taisnstūri tā, lai \(m=2 k(k \geq 2)\) būtu rindu skaits. Lai konstruētu maršrutu, kas apmierina uzdevumu nosacijumus, ieviešam rūtiņu koordinātu sistēmu \((m;n)\), kur \(m\) - rindas numurs, \(n\)-kolonnas numurs un \((1;1)\) ir apakšējais kreisais stūris.
Aplūkojam maršrutu, kas secīgi vienas rindas vai vienas kolonnas ietvaros savieno šādas rūtiņas:
- \((i ; 2)\) ar \((i ; n)\)
- \((i ; n)\) ar \((i+1 ; n)\)
- \((i+1 ; n)\) ar \((i+1 ; 2)\);
- \((i+1 ; 2)\) ar \((i+2 ; 2)\)
kur \(i\) secīgi vienāds ar \(\{1;3;5;\ldots;m-1=2 k-1\}\).
Konstruētais maršruts noslēgsies rūtiņā \((m;2)\). Tālāk vedam maršrutu uz \((m;1)\) un attiecīgi \((1;1)\) pa pirmo kolonnu. Redzams, ka maršruts apmierina uzdevuma nosacījumu. Maršruta piemērs redzams 16. att. ar vērtībām \(m=4\) un \(n=5\).
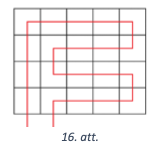
- Ja gan \(m\), gan \(n\) nedalās ar \(2\) (\(m;n \neq 1\)), pierādīsim, ka prasīto maršrutu nav iespējams izveidto. Iekrāsosim taisnstūra rūtiņas šaha galdiņa veidā un ievērosim, ka šādam krāsojumam izpildās īpašība: blakus esošām rūtiņām ir dažādas krāsas.
Pieņemsim pretējo, ka prasītais maršruts eksistē. Tā kā maršruts iziet cauri visām rūtinām, kuru ir nepāra skaits, tad pārejas no vienas rūtiņas uz otru notiek pāra skaitu reižu. Līdz ar to maršruts beigsies tādas pašas krāsas rūtiņā kā sākuma rūtiņa. Taču tā nevar būt, ja šī rūtiņas atrodas blakus, jo tām būtu jābūt dažādās krāsās. Līdz ar to iegūta pretruna un šāds maršruts neeksistē.
Tā kā mainīgos \(m\) un \(n\) uzdevumā kontekstā var mainīt vietām, tad ir aplūkoti visi iespējamie gadījumi.