LV.AMO.2022A.9.3 lv
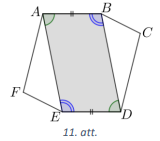
Izliektā sešstūrī \(ABCDEF\) pretējās malas ir pa pāriem paralēlas, tas ir, \(AB \| DE\), \(BC \| EF\) un \(CD \| AF\). Zināms, ka \(AB=DE\). Pierādīt, ka \(BC=EF\) un \(CD=AF\).
Atrisinājums
Novelkam \(AE\) un \(BD\) (skat. 11.att.). Četrstūris \(ABDE\) ir paralelograms, jo \(AB \| DE\) un \(AB=DE\). Tāpēc \(BD=AE, \sphericalangle BAE=\sphericalangle BDE\) un \(\sphericalangle ABD=\sphericalangle AED\).
Tā kā dotā sešstūra pretējās malas ir paralēlas, tad \(\sphericalangle ABC=\sphericalangle DEF\) un \(\sphericalangle CDE=\sphericalangle FAB\) kā leņķi ar paralēlām malām. Tātad iegūstam:
\[\begin{aligned} & \circ \sphericalangle CBD=\sphericalangle ABC-\sphericalangle ABD=\sphericalangle DEF-\sphericalangle AED=\sphericalangle AEF; \\ & \circ \sphericalangle BDC=\sphericalangle CDE-\sphericalangle BDE=\sphericalangle FAB-\sphericalangle BAE=\sphericalangle FAE. \end{aligned}\]
Ievērojam, ka \(\triangle BCD=\triangle EFA\) pēc pazīmes \(\ell m \ell\), jo \(\sphericalangle CBD=\sphericalangle AEF, BD=AE, \sphericalangle BDC=\sphericalangle FAE\). Līdz ar to \(BC=EF\) un \(CD=AF\) kā vienādu trijstūru atbilstošās malas.