LV.AMO.2022A.8.3 lv
Kvadrātā \(ABCD\) novilkta diagonāle \(AC\) un uz tās atzīmēts punkts \(E\) tā, ka \(\sphericalangle DEC=75^{\circ}\). Nogriežņa \(DE\) pagarinājums krusto malu \(AB\) punktā \(F\). Pierādīt, ka \(EF=FB\)!
Atrisinājums
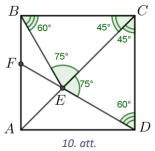
Tā kā \(AC\) ir kvadrāta diagonāle, tad \(\sphericalangle BCA=\sphericalangle DCA=90^{\circ}: 2=45^{\circ}\). No trijstūra \(ECD\) iegūstam, ka \(\sphericalangle EDC=180^{\circ}-45^{\circ}-75^{\circ}=60^{\circ}\).
Novelkam nogriezni \(BE\) (skat. 10.att.). Ievērojam, ka \(\triangle DCE=\triangle BCE\) pēc pazīmes \(m \ell m\), jo \(DC=BC\), \(\sphericalangle ECD=\sphericalangle ECB\), \(EC\) - kopīga. Tā kā vienādos trijstūros attiecīgie elementi ir vienādi, tad \(\sphericalangle BEC=\sphericalangle DEC=75^{\circ}\) un \(\sphericalangle CBE=\sphericalangle CDE=60^{\circ}\).
Aprēķinām \(\sphericalangle FEB=180^{\circ}-\sphericalangle BEC-\sphericalangle DEC=30^{\circ}\) un \(\sphericalangle FBE=90^{\circ}-\sphericalangle CBE=30^{\circ}\). Tātad \(\sphericalangle FEB=\sphericalangle FBE\) un trijstūris \(EFB\) ir vienādsānu. Līdz ar to \(EF=FB\).