Atrisinājums

Tā kā paralelograma pretējās malas ir paralēlas, tad iespējami trīs gadījumi, kā var izvēlēties pretējās malas (skat. 23.att.).

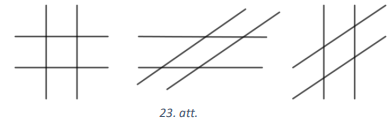
1. Par pretējām malām varam izvēlēties divas no horizontālajām taisnēm (to var izdarīt \(4 \cdot 3:2=6\) veidos) un divas no vertikālajām taisnēm (to var izdarīt \(5 \cdot 4:2=10\) veidos). Līdz ar to šādu paralelogramu skaits ir \(6 \cdot 10=60\).
2. Par pretējām malām varam izvēlēties divas no horizontālajām taisnēm (to var izdarīt \(4 \cdot 3:2=6\) veidos) un divas no slīpajām taisnēm (to var izdarīt \(3 \cdot 2:2=3\) veidos). Līdz ar to šādu paralelogramu skaits ir \(6 \cdot 3=18\).
3. Par pretējām malām varam izvēlēties divas no slīpajām taisnēm (to var izdarīt \(3 \cdot 2:2=3\) veidos) un divas no vertikālajām taisnēm (to var izdarīt \(5 \cdot 4:2=10\) veidos). Līdz ar to šādu paralelogramu skaits ir \(3 \cdot 10=30\). Tātad pavisam ir izveidoti \(60+18+30=108\) paralelogrami.