Atrisinājums

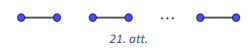
Pamatosim, ka prasītais ir iespējams, ja \(m\) ir pāra skaitlis vai nepāra skaitlis, kas nav mazāks kā \(9\). Ievērojam, ka pirmo divu naturālo skaitļu kubi ir \(1^{3}=1\) un \(2^{3}=8\). Rūķīšus apzīmēsim ar punktiem; ja divi rūķīši draudzējas, tad tos savienosim ar nogriezni.

Ja \(m\) ir pāra skaitlis, tad rūķīšus var sadalīt pāros tā, ka katrs rūķītis draudzējas tikai un vienīgi ar rūķīti no sava pāra (skat. 21.att.).

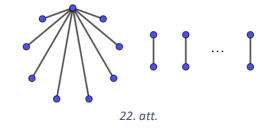
Ja \(m\) ir nepāra skaitlis un \(m \geq 9\), tad rūķīšus var sadalīt tā, kā parādīts 22.att., tas ir, vienam rūķītim ir \(8\) draugi, bet pārējiem pa vienam draugam.

Pamatosim, ka neder tādi nepāra skaitļi \(m\), ka \(m \leq 7\).

Visiem rūķīšiem nevar būt pa vienam draugam, jo tad kopā būtu nepāra skaits nogriežņu galu, bet tas nav iespējams, jo katram nogrieznim ir \(2\) gali. Tātad kādam rūķītim būtu jābūt vismaz \(8\) draugiem, bet arī tas nav iespējams, jo lielākais nogriežņu galu skaits, kas var iziet no kāda punkta, ir \(6\) (gadījumā, ja \(m=7\) ).