LV.AMO.2019.8.3 lv
Dots paralelograms \(ABCD\). Leņķa \(BAD\) bisektrise krusto malu \(BC\) iekšējā punktā \(E\) un \(CD\) pagarinājumu punktā \(F\). Pierādīt, ka \(BC=DF\), ja zināms, ka \(DE\) ir perpendikulārs \(AF\).
Atrisinājums
Ievērojam, ka
- \(\sphericalangle BAE=\sphericalangle EAD=\alpha\) pēc bisektrises definīcijas;
- \(\sphericalangle BAE=\sphericalangle AFD=\alpha\) kā iekšējie šķērsleņķi pie paralēlām taisnēm \(AB\) un \(CD\), ko krusto taisne \(AF\)
Tātad trijstūris \(ADF\) ir vienādsānu trijstūris (skat. 20.att.), kuram \(AD=DF\). Tā kā \(AD=BC\) kā paralelograma pretējās malas, tad esam ieguvuši, ka \(BC=DF\).
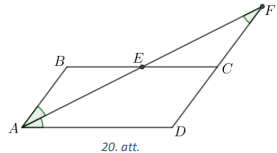
Piezīme. Tas, ka \(DE\) ir perpendikulārs \(AF\), risinājumā nav obligāti jāizmanto.