LV.AMO.2019.7.3 lv
Izliektā četrstūrī \(ABCD\) leņķu \(BAD\) un \(ADC\) bisektrises krustojas punktā \(M\). Pierādīt, ka \(BM=CM\), ja zināms, ka \(AD=AB+CD\).
Piezīme. Četrstūri sauc par izliektu, ja visi tā iekšējie leņķi ir mazāki nekā \(180^{\circ}\).
Atrisinājums
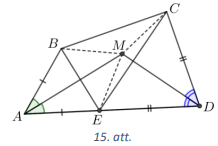
Uz malas \(AD\) atliekam punktu \(E\) tā, ka \(AE=AB\) (skat. 15.att.). Tā kā pēc dotā \(AD=AB+CD\), tad \(ED=CD\). Tātad trijstūri \(BAE\) un \(CDE\) ir vienādsānu trijstūri un attiecīgi bisektrise \(AM\) un \(DM\), kas vilktas no virsotnes leņķa, ir arī mediāna un augstums jeb attiecīgi nogriežņu \(BE\) un \(CE\) vidusperpendikuli. Ja punkts atrodas uz nogriežņa vidusperpendikula, tad tas atrodas vienādā attālumā no nogriežņa galapunktiem. Tātad \(MB=ME\) un \(ME=MC\) (jo \(M\) atrodas uz nogriežņa vidusperpendikula), no kā izriet, ka \(MB=MC\).