LV.AMO.2018.9.5
Kāds ir mazākais rūtiņu skaits, kas jāiekrāso taisnstūrī ar izmēriem \(5 \times 8\) rūtiņas, lai katrā šī taisnstūra \(2 \times 3\) rūtiņu taisnstūrī (tas var būt arī pagriezts vertikāli) būtu vismaz viena iekrāsota rūtiņa?
Atrisinājums
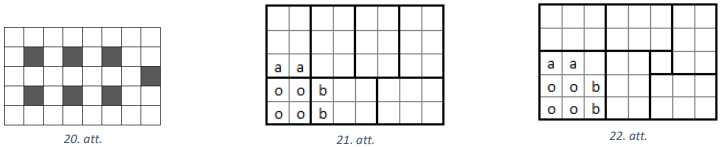
Mazākais rūtiņu skaits, kas jāiekrāso, ir \(7\), skat., piemēram, 20.att.
Pierādīsim, ka ar \(6\) iekrāsotām rūtiņām nepietiek. Sadalām taisnstūri tā, kā parādīts 21.att. Katrā taisnstūrī \(2 \times 3\) jāiekrāso tieši viena rūtiņa (kopā tad būs iekrāsotas \(6\) rūtiņas), bet kvadrātā \(2 \times 2\) nedrīkst iekrāsot nevienu rūtiņu, tāpēc jāiekrāso viena no rūtiņām "\(a\)" un viena no rūtiņām "\(b\)".
Sadalām doto taisnstūri tā, kā parādīts 22.att. Kvadrātā \(3 \times 3\) jau ir iekrāsotas \(2\) rūtiņas un katrā no pieciem taisnstūriem \(2 \times 3\) jāiekrāso vismaz viena rūtiņa. Tātad iekrāsotas ir vismaz \(7\) rūtiņas.
Atrisinājums
Mazākais rūtiņu skaits, kas jāiekrāso, ir \(7\), skat., piemēram, 20.att.
Pierādīsim, ka ar \(6\) iekrāsotām rūtiņām nepietiek. Sadalām taisnstūri sešos taisnstūros \(2 \times 3\) un vienā kvadrātā \(2 \times 2\) (skat. 23.att.). Katrā taisnstūrī \(2 \times 3\) jāiekrāso tieši viena rūtiņa (kopā tad būs iekrāsotas \(6\) rūtiņas), bet kvadrātā \(2 \times 2\) nedrīkst iekrāsot nevienu rūtiņu.
Sadalām doto taisnstūri sešos taisnstūros \(2 \times 3\) un vienā taisnstūrī \(1 \times 4\) (skat. 24.att.). Katrā taisnstūrī \(2 \times 3\) jāiekrāso tieši viena rūtiņa (kopā tad būs iekrāsotas \(6\) rūtiņas), bet taisnstūrī \(1 \times 4\) nedrīkst iekrāsot nevienu rūtiņu (skat. 24.att., kur ar " \(o\) " atzīmētas neiekrāsotās rūtiņas). Redzams, ka ir taisnstūris \(2 \times 3\), kurā nav iekrāsota neviena rūtiņa. Tātad ar \(6\) iekrāsotām rūtiņām nepietiek.
