LV.AMO.2018.9.3 lv
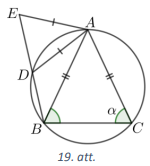
Ap vienādsānu trijstūri \(ABC\) (\(AB=AC\)) apvilkta riņķa līnija. Caur virsotni \(B\) un loka \(AB\) (kas nesatur \(C\)) iekšēju punktu \(D\) novilkta taisne, uz kuras atzīmēts punkts \(E\) tā, ka \(AD=AE\). Pierādīt, ka trijstūri \(ABC\) un \(ADE\) ir līdzīgi!
Atrisinājums
Apzīmējam \(\sphericalangle ACB=\sphericalangle CBA=\alpha\) (skat. 19.att.). Tā kā četrstūris \(ACBD\) ir ievilkts riņķa līnijā, tad tā pretējo leņķu summa ir \(180^{\circ}\), tātad \(\sphericalangle ADB=180^{\circ}-\sphericalangle ACB=180^{\circ}-\alpha\). Izmantojot blakusleņķu īpašību, iegūstam \(\sphericalangle ADE=180^{\circ}-\sphericalangle ADB=180^{\circ}-\left(180^{\circ}-\alpha\right)=\alpha\). Tā kā \(AD=AE\), tad \(\sphericalangle ADE=\sphericalangle DEA=\alpha\). Līdz ar to \(\triangle ABC \sim \triangle AED\) pēc pazīmes \(\ell \ell\).