LV.AMO.2018.8.4 lv
Par maģisko kvadrātu sauc \(n \times n\) rūtiņu tabulu, kuras rūtiņās ierakstīti skaitļi no \(1\) līdz \(n^{2}\) tā, ka visās tabulas rindās, kolonnās un uz abām galvenajām diagonālēm rūtiņās ierakstīto skaitļu summas ir vienādas. (Katrs no skaitļiem ierakstīts tieši vienā rūtiņā.) Vai noteikti maģiskā kvadrāta centrālajā rūtiņā ir ierakstīts skaitlis \(\frac{n^{2}+1}{2}\), ja (A) \(n=3\), (B) \(n=5\)?
Atrisinājums
(A) Jā, var apgalvot. Apzīmējam tabulā ierakstītos skaitļus ar \(a, b, c, d, e, f, g, h\) un \(i\) (skat. 12.att.).

No tā, ka katrā rindā ierakstīto skaitļu summa ir viena un tā pati, var secināt, ka tā ir \(\frac{1+2+3+4+5+6+7+8+9}{3}=15\). Tā kā arī katrā kolonnā un katrā diagonālē ierakstīto skaitļu summa ir \(15\), tad iegūstam, ka \(a+b+c=d+e+f=g+h+i=a+d+g=b+e+h=c+f+i=a+e+i=c+e+g=15\). Ievērojam (skat. 13.att.), ka
\[\begin{gathered} (a+e+i)+(c+e+g)+(b+e+h)-(a+b+c)-(g+h+i)=3e \\ 15 \cdot 3-15 \cdot 2=3e \\ 15=3e \\ e=5 \end{gathered}\]
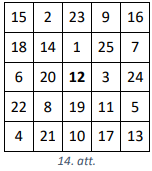
Tātad esam pierādījuši, ka centrālajā rūtiņā vienmēr ir ierakstīts skaitlis \(5\). **(B)** Nē, nevar apgalvot. Centrālajā rūtiņā būtu jābūt \(13\), bet ir iespējams izveidot maģisko kvadrātu, kura centrālajā rūtiņā nav skaitlis \(13\), bet gan ir skaitlis \(12\), skat., piemēram, 14.att., kur atbilstošā summa ir \(65\).