Atrisinājums

Novelkam nogriezni \(EF\), tas sadala doto paralelogramu \(ABCD\) divos vienādos paralelogramos \(ABEF\) un \(FECD\), jo to pretējās malas ir paralēlas un vienādas. Nogriežņu \(BF\) un \(AE\) krustpunktu apzīmējam ar \(G\), bet \(ED\) un \(CF\) krustpunktu - ar \(H\), tad jāaprēķina četrstūra \(FGEH\) laukums (skat. 11.att.).

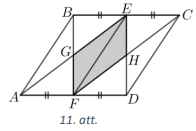
Paralelograma diagonāle sadala paralelogramu divos vienādos trijstūros, tāpēc \(S_{BEF}=\frac{1}{2} S_{ABEF}=\frac{1}{2} \cdot \frac{1}{2} S_{ABCD}=\frac{1}{4} \cdot 100=25\). Tā kā trijstūriem \(BEG\) un \(GEF\) ir kopīgs augstums no virsotnes \(E\) un malas, pret kurām novilkts šis augstums (\(BG\) un \(GF\)), ir vienādas, tad šie trijstūri ir vienlieli, tas ir, to laukumi ir vienādi. Tātad \(S_{GEF}=\frac{1}{2} S_{BEF}=\frac{1}{2} \cdot 25=12.5\). Līdzīgi iegūstam, ka \(S_{FEH}=12.5\). Līdz ar to \(S_{FGEH}=12.5 \cdot 2=25\).