Atrisinājums

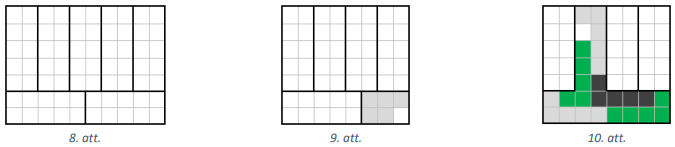
Abi var izgriezt vienādu skaitu figūru. Taisnstūris ar izmēriem \(7 \times 2018\) rūtiņas satur \(7 \cdot 2018=14126\) rūtiņas, tāpēc maksimālais figūru skaits, ko varētu izgriezt, ir \(2825\), jo \(5 \cdot 2825+1=14126\). Parādīsim, ka gan Lauriņa, gan Pēcītis var sagriezt doto taisnstūri tā, ka pāri paliek \(1\) rūtiņa. Ievērojam, ka taisnstūri ar izmēriem \(2 \times 5\) rūtiņas var sagriezt gan Lauriņa, gan Pēcītis (skat. 7.att.).

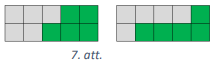
Taisnstūri \(7 \times 2018\) sadalām \(201\) taisnstūrī \(7 \times 10\) un vienā taisnstūrī \(7 \times 8\). Katru taisnstūri \(7 \times 10\) sadalām taisnstūros \(2 \times 5\) tā, kā parādīts 8.att. Lauriņa taisnstūri \(7 \times 8\) var sagriezt tā, kā parādīts 9.att., bet Pēcītis tā, kā parādīts 10.att. Tātad abi var izgriezt vienādu skaitu figūru.