LV.AMO.2017.9.4 lv
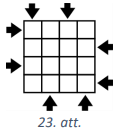
(A) Pierādi, ka dotajā \(4 \times 4\) rūtiņu laukumā (skat. 23.att.) nevar ierakstīt \(16\) dažādus naturālus skaitļus tā, lai katrā rūtiņā būtu ierakstīts viens skaitlis un katrā rindā un katrā kolonnā skaitļi pieaugtu bultiņas norādītajā virzienā.
(B) Kāds mazākais bultiņu skaits jāapvērš pretējā virzienā, lai skaitļus varētu izvietot saskaņā ar uzdevuma nosacījumiem?
Atrisinājums
(A) Apzīmējam rūtiņās ierakstītos skaitļus tā, kā parādīts 24.att. Ievērojam, ka
- \(A_{1} < A_{2}\) (no \(1.\) rindas);
- \(A_{2} < A_{3}\) (no \(3.\) kolonnas);
- \(A_{3} < A_{4}\) (no \(2.\) rindas);
- \(A_{4} < A_{1}\) (no \(2.\) kolonnas).
Līdz ar to esam ieguvuši, ka vienlaicīgi jāizpildās nevienādībām \(A_{1} < A_{4}\) un \(A_{4} < A_{1}\). Tas nav iespējams, tāpēc rūtiņās skaitļus ierakstīt nevar.
(B) Jāapvērš vismaz divas bultiņas. Šajā laukumā var atrast trīs četru rūtiņu ciklus, kas atzīmēti ar burtiem \(A\), \(B\) un \(C\) (skat. 24.att.). Katrai ciklā iesaistītajai bultiņai ir pierakstīts tā cikla burts (vai burti), kurā tā iesaistīta. Līdzīgi kā (A) gadījumā par ciklu \(A\), iegūstam pretrunu arī par ciklu \(B\) un \(C\).
Lai skaitļus rūtiņās varētu ierakstīt, nepieciešams izjaukt visus trīs ciklus. To nav iespējams izdarīt apvēršot tikai vienu bultiņu (nav bultiņas, kas būtu iesaistīta visos trīs ciklos), tāpēc mazākais apvēršamo bultiņu skaits ir divas. Apvēršot divas bultiņas: otrajā rindā un trešajā kolonnā, skaitļus var ierakstīt, piemēram, tā, kā parādīts 25.att.