LV.AMO.2017.8.3 lv
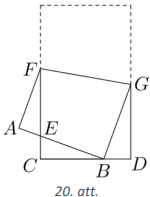
Taisnstūrveida papīra lapu pārlocīja tā, ka pārlocītais lapas stūris atrodas uz pretējās malas (skat. 20.att.). Trijstūri \(AFE\) un \(CBE\) ir vienādi un \(CB=7~\mathrm{cm}\), bet \(BD=3~\mathrm{cm}\). Kādi ir sākotnējās papīra lapas malu garumi?
Atrisinājums
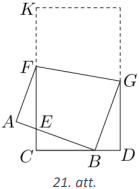
Sākotnējās lapas vienas malas garums \(CD=CB+BD=10~\mathrm{cm}\) (skat. 21.att.). Ievērojam, ka \(AB=CD=10~\mathrm{cm}\) kā pārlocītās taisnstūrveida lapas pretējā mala.
Tā kā pēc dotā trijstūri \(AFE\) un \(CBE\) ir vienādi, tad to atbilstošie elementi arī ir vienādi: \(\sphericalangle AEF=\sphericalangle BEC\), \(AF=CB=7~\mathrm{cm}\), \(AE=EC\) un \(EF=BE\). Saskaitot vienādus lielumus, iegūstam vienādas summas, tas ir, \(CE+EF=AE+EB=AB=10~\mathrm{cm}\). Nogriežņa \(KF\) garums sakrīt ar \(AF\) garumu. Tātad taisnstūra otras malas garums ir \(10+7=17~\mathrm{cm}\). Līdz ar to sākotnējās papīra lapas malu garumi ir \(10~\mathrm{cm}\) un \(17~\mathrm{cm}\).