LV.AMO.2017.8.2 lv
Vai katrā tukšajā aplītī (skat. 17.att.) var ierakstīt vienu naturālu skaitli tā, lai aplīšos būtu ierakstīti visi naturālie skaitļi no \(1\) līdz \(9\) un lai skaitļu summa uz katras trijstūra malas būtu (A) \(22\); (B) \(23\)?
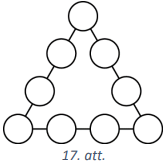
Atrisinājums
(A) Nav iespējams. Virsotnēs ierakstītos skaitļus apzīmēsim ar \(a,\ b,\ c\) (skat. 18.att.), skaitļu summu uz katras trijstūra malas apzīmēsim ar \(S\). Aprēķināsim kopējo skaitļu summu visām trim trijstūra malām, ievērojot, ka skaitļi \(a,\ b\) un \(c\) tiek pieskaitīti divas reizes:
\(3 \cdot S=1+2+2+4+5+6+7+8+9+a+b+c\) jeb \(3S=45+a+b+c\)
Ja \(S=22\), tad virsotņu aplīšos ierakstīto skaitļu summa ir \(a+b+c=21\). Iegūstam, ka \(c=21-a-b\). Neviena no \(a,\ b\) un \(c\) vērtībām nevar būt \(1\), jo pat tad, ja abās pārējās virsotnēs būs ierakstīti abi lielākie atlikušie skaitļi, šo skaitļu summa nepārsniegs \(1+9+8=18\). Tātad skaitlis \(1\) būtu jāieraksta kādā no pārējiem aplīšiem, kas atrodas uz trijstūra malas. Pieņemsim, ka šīs malas virsotnes aplīšos ierakstīti \(a\) un \(b\). Tad otrajā šīs malas aplītī būtu jāieraksta skaitlis \(22-a-b-1=21-a-b\), bet šāda jau ir \(c\) vērtība un šis skaitlis jau ir ierakstīts trešajā virsotnes aplītī. Esam ieguvuši pretrunu, tāpēc \(S\) vērtība nevar būt \(22\).
(B) Jā, prasītais ir iespējams, skat., piemēram, 19.att.
