Atrisinājums

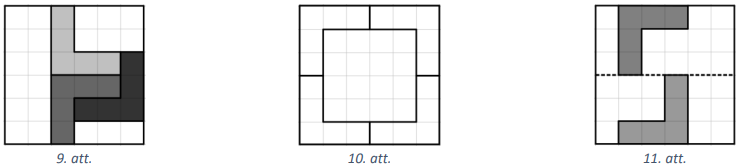
Mazākais skaits stūrīšu, kas jāizgriež, ir \(3\), skat., piemēram, 9.att. Pamatosim, ka ar mazāk kā \(3\) stūrīšiem nepietiek. Pieņemsim, ka pietiek ar \(2\) stūrīšiem. Aplūkojam tās četras iespējamās stūrīšu izgriešanas vietas, kas parādītas 10.att. Ar vienu stūrīti vienlaikus var nosegt ne vairāk kā divas no šīm blakus esošajām stūrišu vietām, turklāt stūrīša malai jāiet pa laukuma malas rūtiņām (pretējā gadīumā stūrītis nevar vienlaikus ietekmēt divas iespējamās stūrīšu novietošanas vietas). Tātad vienam no diviem stūrīšiem jānosedz divas augšējās stūrīšu vietas, bet otram - divas apakšējās. Tas nozīmē, ka augšējā laukuma pusē esošais stūrītis neietekmē apakšējās laukuma puses rūtiņas un otrādi (skat., piemēram, 11.att.), bet, neatkarīgi no tā, kā laukuma augšējā un apakšējā pusē būs novietots katrs no abiem stūrīšem, no katras laukuma puses (augšējās un apakšējās) var izgriezt vēl pa vienam stūrītim. Tātad ar diviem stūrīšiem nepietiek.