Atrisinājums

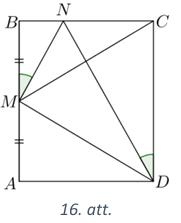
Tā kā \(M\) ir \(AB\) viduspunkts, tad simetrijas dēļ \(CM=MD\) (skat. 16.att.). Tad pietiek pierādīt, ka \(MD=CD\). Trijstūri \(BMN\) un \(CDN\) ir līdzīgi pēc pazīmes \(\ell \ell\), jo \(\sphericalangle MBN=\sphericalangle DCN=90^{\circ}\) un \(\sphericalangle BMN=\sphericalangle CDN\) pēc dotā. Trijstūru līdzības koeficients ir \(\frac{BM}{CD}=\frac{1}{2}\), tāpēc \(CN=2BN\). Bet \(MN=2BN\), jo katete pret \(30^{\circ}\) leņķi ir puse no hipotenūzas. Tāpēc \(\quad MN=CN\). Tā kā \(\quad \sphericalangle BNM=\sphericalangle CND=90^{\circ}-30^{\circ}=60^{\circ}\), tad \(\sphericalangle MND=180^{\circ}-\sphericalangle BNM-\sphericalangle CND=60^{\circ}\). Ievērojot, ka \(ND\) ir trijstūru \(MND\) un \(CND\) kopīga mala, iegūstam, ka \(\triangle MND=\triangle CND\) pēc pazīmes \(m \ell m\). Tad \(MD=CD\). Līdz ar to esam pierādījuši, ka \(MD=CD=CM\) jeb trijstūris \(CDM\) ir vienādmalu.

Piezīme. Apzīmējot \(BM=x, CD=2x\) un izmantojot trigonometriskās sakarības, var izteikt, \(BN=\frac{x \sqrt{3}}{3}\) un \(CN=\frac{2x \sqrt{3}}{3}\). Lietojot Pitagora teorēmu \(\triangle MBC\), iegūstam, ka \(CM=2x\).