LV.AMO.2016.8.5 lv
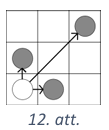
Divi spēlētāji spēlē spēli uz \(N \times N\) rūtiņas liela laukuma. Sākumā laukuma kreisajā apakšējā rūtiņā atrodas spēļu kauliņš. Katrā gājienā spēļu kauliņu drīkst pārvietot vai nu vienu lauciņu pa labi, vai vienu lauciņu uz augšu, vai arī divus lauciņus pa diagonāli uz augšu pa labi (skat. 12.att., kur kauliņa sākumpozīcija apzīmēta ar baltu, bet atļautie gājieni -- ar pelēkiem aplīšiem). Kauliņu nedrīkst pārvietot ārpus laukuma robežām. Spēlētāji gājienus izdara pēc kārtas. Zaudē spēlētājs, kurš nevar izdarīt gājienu. Kurš no spēlētājiem, pareizi spēlējot, uzvar, ja (A) \(N=7\), (B) \(N=8\)?
Atrisinājums
Analizēsim spēli no beigām. Skaidrs, ka laukuma labā augšējā stūra rūtiņa ir zaudējoša, jo no tās nevar izdarīt gājienu. Tālāk laukuma rūtiņas aizpildīsim pēc šāda principa: ja kāds no iespējamajiem gājieniem pārvieto kauliņu uz zaudējošu rūtiņu (apzīmējam ar \(Z\)), tad šī rūtiņa ir uzvaroša (apzīmējam ar \(U\)). Pretējā gadījumā rūtiņa ir zaudējoša. Tādā veidā aizpildot rūtiņas, iegūstam, ka gan (A), gan (B) gadījumā sākuma (kreisā apakšējā stūra rūtiņa) ir zaudējoša, skat. attiecīgi 13.att. un 14.att.
Tātad, pareizi spēlējot, uzvarēs otrais spēlētājs, jo viņš vienmēr var panākt, ka pirmajam spēlētājam gājiens jāizdara no zaudējošas rūtiņas.
