LV.AMO.2016.8.4 lv
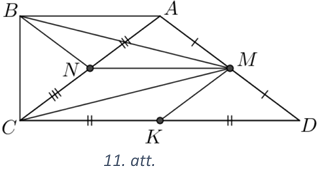
Dota taisnleņķa trapece \(ABCD\), kuras īsākā sānu mala ir \(BC\). Malu \(AD\) un \(CD\) viduspunkti attiecīgi ir \(M\) un \(K\), bet diagonāles \(AC\) viduspunkts ir \(N\). Pierādīt, ka \(\triangle MNB=\triangle CKM\).
Atrisinājums
Nogrieznis \(MN\) ir trijstūra \(CAD\) viduslīnija (skat. 11.att.), tāpēc \(NM=\frac{1}{2} CD=CK\) un \(NM \| CD\). Tā kā \(NM \| CD\) un \(AM=MD\), tad \(NM\) atrodas uz malas \(BC\) vidusperpendikula. No vidusperpendikula īpašības (katrs vidusperpendikula punkts atrodas vienādā attālumā no nogriežņa galapunktiem) iegūstam, ka \(CN=BN\) un \(CM=BM\). Nogrieznis \(MK\) ir trijstūra \(CAD\) viduslīnija, tāpēc \(MK=\frac{1}{2} AC=CN\). Līdz ar to esam ieguvuši, ka \(\triangle MNB=\triangle CKM\) pēc pazīmes \(mmm\).