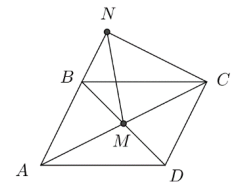
Atrisinājums

Ievērojam, ka \(\triangle ABD=\triangle CDB\) pēc pazīmes \(\ell m \ell\), jo \(\sphericalangle ABD=\sphericalangle CDB\) kā iekšējie šķērsleņķi pie paralēlām taisnēm, \(BD\) -- kopīga mala un \(\sphericalangle ADB=\sphericalangle CBD\) kā iekšējie šķērsleņķi pie paralēlām taisnēm (skat. 10.att.).

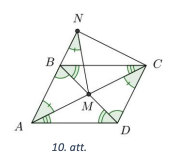
Tātad \(AD=BC\) kā vienādu trijstūru atbilstošās malas. Līdzīgi \(\triangle AMD=\triangle CMB\) pēc pazīmes \(\ell m \ell\), jo \(\sphericalangle MAD=\sphericalangle MCB, AD=BC\) un \(\sphericalangle ADM=\sphericalangle CBM\), tātad \(AM=MC\). Trijstūri \(AMN\) un \(NMC\) ir vienādsānu, tāpēc \(\sphericalangle MAN=\sphericalangle ANM\) un \(\sphericalangle MNC=\sphericalangle MCN\). Tā kā \(\sphericalangle MAN=\sphericalangle ACB\), tad \(\sphericalangle ANC=\sphericalangle NCD\). Esam ieguvuši, ka iekšējie vienpusleņķi pie paralēlām taisnēm \(AN\) un \(CD\) ir vienādi, tātad \(\sphericalangle ANC=90^{\circ}\).