Atrisinājums

(A) Der, piemēram, virkne

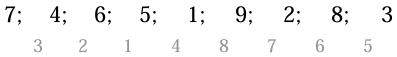
(B) Aplūkosim skaitļu virkni \(1; 2015; 2; 2014; 3; 2013; 4; 2012; ...; 1007; 1009; 1008\) (šī virkne sastāv no divām virknēm -- vienas augošas \(1 ; 2 ; 3 ; \ldots ; 1008\) un otras dilstošas \(2015; 2014; \ldots; 1009\)). Šajā virknē ir visi skaitļi no \(1\) līdz \(2015\) un starpības starp katriem diviem blakus esošiem skaitļiem dilst no \(2014\) līdz \(1\). Šī virkne pēc savām īpašībām ir ļoti līdzīga nepieciešamajai, tikai skaitlis \(1\) šajā virknē ir pirmais nevis \(1008.\) loceklis. Virknes \(1008.\) loceklis (jeb 504.loceklis dilstošajā virknē) ir \(a_{504}=2015+(-1)(504-1)=1512\), virknes \(1009.\) loceklis (jeb \(505.\) loceklis augošajā virknē) ir \(505\). Starpība starp virknes \(1008.\) un \(1009.\) locekli ir \(1512-505=1007\). „Pārgriezīsim” izveidoto virkni starp \(1008.\) un \(1009.\) elementu, iegūstot divus virknes fragmentus, no kuriem pirmais satur \(1008\) locekļus, bet otrais satur \(1007\) locekļus. No sākotnējām blakus elementu starpībām ir pazaudēta tikai „pārgrieztā” starpība \(1007.\) Tagad saliksim šos fragmentus pretējā secībā- tā, ka vispirms ir fragments, kurā ir \(1007\) skaitļi un kurš beidzas ar skaitli \(1008\), un pēc tam fragments, kurā ir \(1008\) skaitļi un kurš sākas ar skaitli \(1\). „Salīmēsim" šos fragmentus kopā, iegūstot trūkstošo starpību \(1007\). Vajadzīgā virkne ir izveidota, skaitlis \(1\) ir jaunās virknes \(1008.\) loceklis un starp blakus elementu starpībām atrodami visi skaitļi no \(1\) līdz \(2014\):