LV.AMO.2015.9.4 lv
Vienādsānu trapeces \(ABCD\) sānu malas ir \(AB\) un \(CD\), bet diagonāles \(AC\) un \(BD\) krustojas punktā \(E\). Ap trijstūri \(CDE\) apvilktā riņķa līnija krusto garāko pamatu \(AD\) iekšējā punktā \(F\). Nogriežņu \(CF\) un \(BD\) krustpunkts ir \(G\). Nosaki \(\sphericalangle CGD\) lielumu, ja \(\sphericalangle CAD=\alpha\)!
Atrisinājums
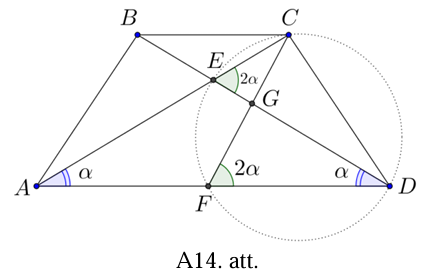
Tā kā trapece \(ABCD\) ir vienādsānu, tad arī \(\sphericalangle ADE=\alpha\) (skat. A14.att.). No trijstūra \(AED\) iegūstam, ka \(\sphericalangle AED=180^{\circ}-2 \alpha\). Izmantojot blakusleņķu īpašīu, iegūstam, ka \(\sphericalangle CED=2 \alpha\). Punkti \(C, E, F\), \(D\) atrodas uz vienas riņķa līnijas, tāpēc \(\sphericalangle CED=\sphericalangle CFD=2 \alpha\) kā ievilktie leņķi, kas balstās uz viena loka \(CD\). No trijstūra \(FGD\) iegūstam, ka \(\sphericalangle FGD=180^{\circ}-3 \alpha\) un šī leņķa blakusleņķis \(\sphericalangle CGD=3 \alpha\).