Atrisinājums

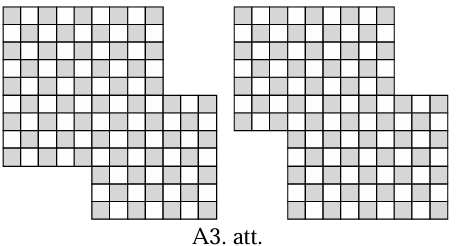
Nē, prasīto izdarīt nevar. Ir divi dažādi veidi, kā no kvadrāta pretējiem stūriem var izgriezt \(3 \times 5\) rūtiņu taisnstūrus: 1) viens novietots horizontāli, otrs- vertikāli, 2) abi novietoti vienā virzienā. Iekrāsosim atlikušo figūru kā šaha galdiņu. Neatkarīgi no tā, kā ir izgriezti taisnstūri, figūrā ir \(58\) melnas un \(56\) baltas rūtiņas (skat. A3.att.). Lai kur novietotu domino kauliņu, tas vienmēr pārklās tieši vienu melnu un tieši vienu baltu rūtiņu. Līdz ar to \(57\) domino kauliņi pārklās vienāda skaita melno un balto rūtiņu. Iegūta pretruna, jo figūrā nav vienāds skaits melno un balto rūtiņu.