Atrisinājums

Ja \(n\)- nepāra skaitlis, tad kvadrāts \(n \times n\) satur nepāra skaita rūtiņas, kas nedalās ar \(4\)- rūtiņu skaitu taisnstūrī. Tātad \(n\) jābūt pāra skaitlim. Aplūkosim divus iespējamos gadījumus.

• Ja \(n=4k\) (\(k\)- naturāls skaitlis), tad kvadrātu ir iespējams sagriezt prasīajā veidā, piemēram, vispirms kvadrāu sagriež pa rindām (taisnstūros \(1 \times 4k\) ) un tad katru rindu \(k\) taisnstūros, kuru izmēri ir \(1 \times 4\).
• Ja \(n=4k+2\) (\(k\)- naturāls skaitlis), tad izkrāsosim kvadrātu četrās krāsās diagonālveidā (skat. A15.att.). Lai kā arī grieztu, taisnstūris \(1 \times 4\) vienmēr saturēs visu četru krāsu rūtiņas. Tātad kvadrātā visu krāsu rūtiņām ir jābūt vienādā skaitā. Noskaidrosim, cik katras krāsas rūtiņu ir kvadrātā. Tā kā kvadrātu \(4k \times 4k\) var sagriezt taisnstūros \(1 \times 4\), tad tajā visu krāsu rūtiņas ir vienādā skaitā. Pēdējās divas kolonnas un rindas dalām taisnstūros \(4 \times 2\), arī tajos visu krāsu rūtiņas ir vienādā skaitā, jo katru no tiem var sadalīt divos taisnstūros \(1 \times 4\). Vēl paliek kvadrāts \(2 \times 2\), kurā dzeltenās krāsas rūtiņa nav vispār un ir divas baltās rūtiņas. Iegūta pretruna ar to, ka kvadrātā visu krāsu rūtiņas ir vienādā skaitā. Līdz ar to kvadrātu, kura malas garums ir \(n=4k+2\), nav iespējams sagriezt taisnstūros ar izmēriem \(1 \times 4\) rūtiņas.

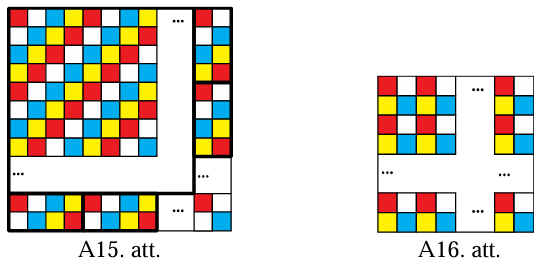
Esam ieguvuši, ka vienīgais gadījums, kad kvadrātu \(n \times n\) rūtiņas var sagriezt taisnstūros ar izmēriem \(1 \times 4\), ja \(n=4k\), kur \(k\)- naturāls skaitlis.

Piezīme. Gadījumā, kad \(n=4k+2\) (\(k\)- naturāls skaitlis), kvadrātu varēja izkrāsot četrās krāsās tā, kā parādīts A16.att. Tad, lai kā arī grieztu, taisnstūris \(1 \times 4\) vienmēr saturēs tieši divas vienas krāsas un tieši divas citas krāsas rūtiņas. Tātad kvadrātā katras krāsas rūtiņām ir jābūt pāra skaitā, kas ir pretruna tam, ka katras krāsas rūtiņu skaits kvadrātā ir \(\frac{(4k+2)^{2}}{4}=(2k+1)^{2}=4k^{2}+4k+1\), kas ir nepāra skaitlis.