LV.AMO.2014.9.4 lv
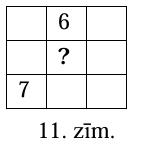
Tabulas \(3 \times 3\) rūtiņās katrā rūtiņā jāieraksta pa vienam naturālam skaitlim tā, lai katrā rindā, katrā kolonnā un katrā diagonālē ierakstīto skaitļu summas būtu vienādas, bet visi tabulā ierakstītie skaitļi ir savā starpā atšķirīgi. Ir zināmi divās rūtiņās ierakstītie skaitļi (skat. 11.zīm.). Kāds ir mazākais skaitlis, kas var būt ierakstīts tabulas centrālajā rūtiņā?
Atrisinājums
Apzīmēsim skaitli, kas atrodas vidējās kolonnas vidējā rūtiņā ar \(x\), bet apakšējā- ar \(y\). Tad visu rindu, kolonnu un diagonāļu summas ir \(6+x+y\). Tālāk tabulas rūtiņas var aizpildīt šādi:
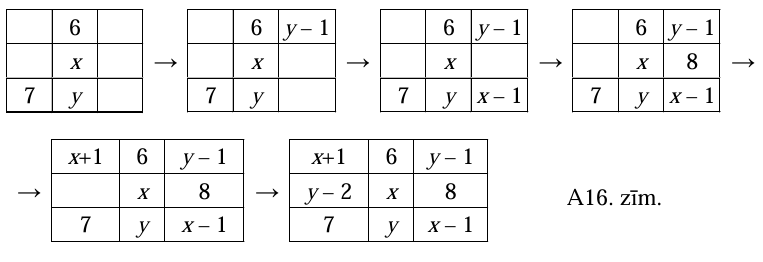
Vienas diagonāles skaitļu summa ir \(3x\). Tātad \(y=2x-6\).

Atliek izvēlēties tādu mazāko \(x\), lai visi tabulā ierakstītie skaitļi būtu naturāli un savā starpā atšķirīgi. Jāizpildās nevienādībai \(2x-8 > 0\) jeb \(x > 4\).
Apskatām iespējamās \(x\) vērtības:
- \(x=5\) neder, jo \(x+1=6\), bet tabulā jau ir ierakstīts skaitlis \(6\);
- \(x=6, x=7\) un \(x=8\) neder, jo tabulā jau ir ierakstīti skaitļi \(6, 7, 8\);
- \(x=9\) neder, jo \(x-1=8\), bet tabulā jau ir ierakstīts skaitlis \(8\);
- \(x=10\) der un aizpildīta tabula parādīta A18.zīm.
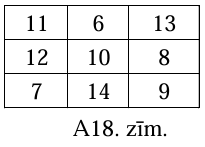
Līdz ar to mazākais skaitlis, kas var būt ierakstīts tabulas centrālajā rūtiņā, ir \(10\).