LV.AMO.2014.9.1
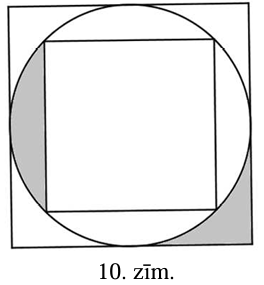
Kvadrātā, kura malas garums ir \(2\), ievilkts riņķis un šajā riņķī ievilkts kvadrāts (skat. 10.zīm.). Aprēķināt iekrāsoto daļu laukumu summu!
Atrisinājums
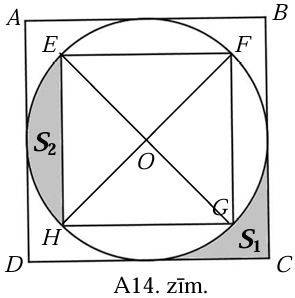
Ievilktā riņķa rādiusa garums ir puse no kvadrāta \(ABCD\) malas garuma, t.i., \(EO=FO=\frac{1}{2} AB=1\). Izmantojot Pitagora teorēmu trijstūrī \(EOF\) (skat. A14.zīm.), iegūstam \(EF=\sqrt{EO^{2}+FO^{2}}=\sqrt{2}\).
Aprēķinām katras iekrāsotās daļas laukumu:
- \(S_{1}=\frac{1}{4}\left(S_{ABCD}-S_{O}\right)=\frac{1}{4}\left(AB^{2}-\pi \cdot EO^{2}\right)=\frac{1}{4}(4-\pi)\);
- \(S_{2}=\frac{1}{4}\left(S_{\mathrm{O}}-S_{EFGH}\right)=\frac{1}{4}\left(\pi \cdot EO^{2}-EF^{2}\right)=\frac{1}{4}(\pi-2)\).
Līdz ar to \(S_{1}+S_{2}=\frac{1}{4}(4-\pi)+\frac{1}{4}(\pi-2)=\frac{4-\pi+\pi-2}{4}=\frac{1}{2}\).