LV.AMO.2014.8.4 lv
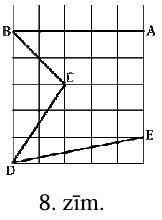
Rūtiņu lapā rūtiņu virsotnēs atzīmēti punkti \(A, B, C, D, E\) un novilkti nogriežņi \(AB, BC, CD\) un \(DE\) (skat. 8.zīm.). Kurš no leņķiem \(\sphericalangle ABC\) un \(\sphericalangle CDE\) ir lielāks?
Atrisinājums
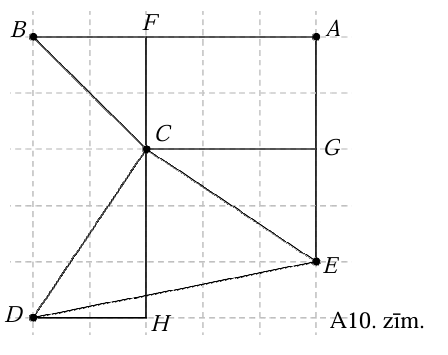
Ievērojam, ka trijstūris \(BFC\) ir vienādsānu taisnleņķa trijstūris (skat. A10.zīm.), tāpēc \(\sphericalangle ABC=45^{\circ}\).
Trijstūri \(DHC\) un \(EGC\) ir vienādi pēc pazīmes „ \(mm \ell\) ”, tāpēc \(CD=CG\) un \(\sphericalangle CDH= \sphericalangle ECG\) kā atbilstošās malas un leņķi. Iegūst, ka \(\sphericalangle DCE=\sphericalangle DCH+\sphericalangle HCE=\sphericalangle ECG+\sphericalangle HCE=90^{\circ}\). Tātad arī trijstūris \(DCE\) ir vienādsānu taisnleņķa trijstūris, tāpēc \(\sphericalangle CDE=45^{\circ}\). Līdz ar to esam parādījuši, ka \(\sphericalangle ABC=\sphericalangle CDE=45^{\circ}\).