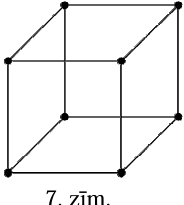
Atrisinājums

Apskatām kuba augšējo un apakšējo skaldni. Izvēlēto punktu skaitu no augšējās skaldnes apzīmēsim ar \(a\), bet no apakšējās- ar \(b\). Tad \(a+b=5\) un \(a \neq b\). Varam pieņemt, ka \(a > b\), tāpēc \(a \geq 3\) un \(a\) var būt \(3\) vai \(4\).

Apskatām abus gadījumus:

• Ja \(a=4\), tad augšējie \(4\) punkti savā starpā jau ir savienoti ar \(4\) šķautnēm.
• Ja \(a=3\), tad šie augšējie trīs punkti ir savienoti ar \(4-2=2\) šķautnēm. Savukārt kāds no apakšējiem diviem punktiem neatradīsies zem tās augšējās kuba virsotnes, kas netika izvēlēta. Tāpēc tas atradīsies zem kāda jau izvēlēta punkta un būs vertikāla kuba šķautne, kurai abi gali ir izvēlētie punkti. Tāpēc kopā būs vismaz \(2+1=3\) šķautnes, kas tos savieno.

Līdz ar to esam pierādījuši prasīto.