LV.AMO.2012.7.5 lv
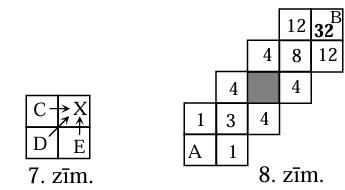
Figūriņa zilonis var pārvietoties vienu rūtiņu uz augšu, vienu rūtiņu pa labi vai vienu rūtiņu pa diagonāli (skat. 2.zīm.). Cik dažādos veidos zilonis no rūtiņas \(A\) var nokļūt rūtiņā \(B\) (skat. 3.zīm.)? Iekrāsotajā rūtiņā ir šķērslis, tajā zilonis nedrīkst iet.
Atrisinājums
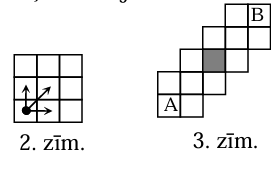
Pakāpeniski aprēķināsim, cik veidos zilonis var nokļūt katrā rūtiņā. Ievērosim: ja rūtiņās \(C, D\) un \(E\) var nokļūt attiecīgi \(c, d\) un \(e\) veidos, tad rūtiņā \(X\) var nokļūt \(x=c+d+e\) veidos (skat. 7.zīm.). Tātad no rūtiņas \(A\) rūtiņā \(B\) var nokļūt \(32\) veidos (skat. 8.zīm.).