LV.AMO.2011.9.2 lv
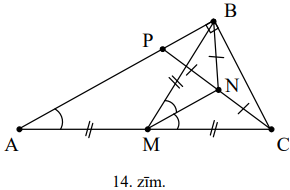
Trijstūrī \(ABC\ \sphericalangle ABC=90^{\circ}\), bet punkts \(P\) atrodas uz malas \(AB.\ M\) un \(N\) ir attiecīgi \(AC\) un \(PC\) viduspunkti. Pierādi, ka \(\sphericalangle BAC=\sphericalangle BMN\).
Atrisinājums
Tā kā \(\triangle ABC\) un \(\triangle PBC\) ir taisnleņķa, \(AM=BM=CM\) un \(PN=BN=CN\) (skat. 14.zīm.). Tāpēc \(\Delta MBN=\triangle MCN\) (pazīme \(mmm\)) un \(\sphericalangle BMN=\sphericalangle CMN\), jo vienādos trijstūros pret vienādām malām ir vienādi leņķi. \(MN\) ir \(\triangle APC\) viduslīnija, tāpēc \(AP \parallel MN\) un \(\sphericalangle CMN=\sphericalangle CAP\) kā kāpšļu leņķi. Tātad, \(\sphericalangle BMN=\sphericalangle CMN=\sphericalangle CAP=\sphericalangle BAC\), k.b.j.