Atrisinājums

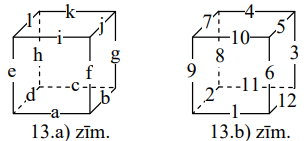
Apzīmēsim ierakstos skaitļus kā parādīts \(13\). a) zīm. Tad

\[\begin{aligned} & S=a+b+c+d \\ & S=a+e+i+f \\ & S=b+g+j+f \\ & S=c+g+k+h \\ & S=d+h+l+e \\ & S=i+j+k+l \end{aligned} \]

Saskaitot šīs vienādības, iegūstam \(6S=2(a+b+c+d+e+f+g+h+i+j+k+l)=2 \cdot \frac{(1+12) \cdot 12}{2}=12 \cdot 13\) un \(S=26\)

1. b) zīm. parādīts piemērs, kā to realizēt.