LV.AMO.2011.8.2 lv
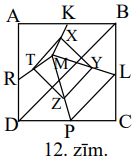
Kvadrāta iekšpusē izvēlēts patvaļīgs punkts \(M\), bet \(K,\ L,\ P,\ R\) ir kvadrāta malu viduspunkti. Pierādi, ka četrstūris, ko veido nogriežņu \(MK,\ ML,\ MP\) un \(MR\) viduspunkti, ir kvadrāts.
Atrisinājums
No viduslīniju īpašības trijstūros \(MZY\) un \(BCD\) seko \(ZY=\frac{1}{2} PL=\frac{1}{2}\left(\frac{1}{2} BD\right)=\frac{1}{4} BD\) (skat. 12.zīm.), līdzīgi \(TX=\frac{1}{4} BD=ZY\), pie tam \(ZY \parallel TX\). Līdzīgi pierāda, ka \(XY \parallel ZT\) un \(TZ=XY=\frac{1}{4} AC\). Bet \(AC=BD\), tātad \(TZ=XY=ZY=TX\) un \(TXYZ\) ir rombs. Tā kā \(BD \perp AC\) un \(TX \parallel BD,\ XY \parallel C\), tad \(TX \perp XY\) un \(TXYZ\) ir kvadrāts, k.b.j.