Atrisinājums

Ar \(f_{n}\) apzīmēsim cik veidos taisnstūri \(3 \times n\) var sadalīt taisnstūros \(1 \times 3\).

\(f_{1}=1, \quad f_{2}=1, \quad f_{3}=2\).

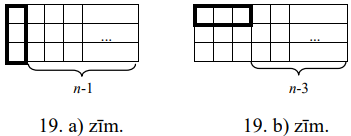
Apskatām taisnstūri ar izmēriem \(3 \times n\). Pirmo taisnstūrīti \(1 \times 3\) varam novietot a) "vertikāli" (skat. 19. a) zīm.) vai b) "horizontāli" (skat. 19. b) zīm.). a) gadījumā neaizpildīts paliek taisnstūris \(3 \times(n-1)\), ko var aizpildīt \(f_{n-1}\) veidos. b) gadījumā vēl divi taisnstūriši \(1 \times 3\) jānovieto "horizontāli" (nevienu "vertikāli" ievietot nav iespējams), tad neaizpildīts paliks taisnstūris \(3 \times(n-3)\), ko var aizpildīt \(f_{n-3}\) veidos.

Tātad \(f_{n}=f_{n-1}+f_{n-3}\). Izmantojot šo rekursīvo sakarību viegli aprēķināt, ka \(f_{12}=70\).