LV.AMO.2010.6.3 lv
(A) Dots, ka taisnstūri ar izmēriem \(m \times n\) rūtiņas var sagriezt tādās figūrās, kāda redzama 4.zīm. Pierādīt: šo taisnstūri var sagriezt arī tādās figūrās, kāda redzama 5.zīm.
(B) Vai taisnība, ka jebkuru taisnstūri, kam gan garums, gan platums ir vismaz \(4\) rūtiņas un kuru var sagriezt 6.zīm. redzamās figūrās, var sagriezt arī 7.zīm. redzamās figūrās?

Figūras var būt arī pagrieztas vai apgrieztas "uz mutes".
Atrisinājums
(A) no dotā seko, ka \(m \cdot n\) dalās ar \(5\). Tātad vai nu \(m\), vai \(n\) dalās ar \(5\). Varam pieņemt, ka \(n\) dalās ar \(5\). Tad sagriežam taisnstūri strēmelēs \(1 \times n\) un pēc tam šīs strēmeles - gabalos \(1 \times 5\).
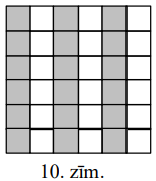
(B) nē. Kvadrātu \(6 \times 6\) var sagriezt kvadrātos \(2 \times 2\). Pierādīsim, ka to nevar sagriezt \(L\) - tetramino. Iekrāsosim kvadrāta rūtiņas, kā parādīts 10.zīm. Katrs \(L\) - tetramino satur vai nu \(3\), vai \(1\) melnu rūtiņu. Tāpēc \(9\ L\) - tetramino kopā satur nepāra skaitu melnu rūtiņu. Bet melno rūtiņu pavisam ir \(18\).