Atrisinājums

Izmantosim matemātisko indukciju. Pie \(n=1\) un \(n=2\) apgalvojums acīmredzami pareizs. Pieņemsim, ka tas pareizs pie \(n<k\), un apskatīsim gadījumu, kad \(n=k\). Pieņemsim, ka kreisajā rindas galā jābūt 1.sējumam utt.; labajā galā jābūt \(n\)-tajam sējumam.

Attēlosim situācijas tā, kā parādīts 25.zīm.: zem svītras norādītas sējumu atrašanās vietas, virs svītras - to sējumu numuri, kas kādā brīdī atrodas atbilstošajās vietās (sējumu numuri apvilkti ar aplīšiem):

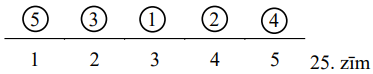
Sāksim "bīdīt" \(k\)-to sējumu pa labi, mainot to ar kārtējiem kaimiņiem, kamēr kārtējās maiņas rezultātā kārtējais kaimiņš "nedraud" nostāties savā vietā. Ja šāda iespēja parādās, šķirojam gadījumus:

A. Šīs maiņas rezultātā arī \(k\)-tais sējums nostātos savā vietā. Tad šo maiņu izdarām. Rezultātā \((k-1)\)-ais un \(k\)-tais sējumi ir savās vietās, bet citi sējumi - joprojām nē. Esam ieguvuši situāciju ar \(n=k-2\) un varam atsaukties uz induktīvo hipotēzi.

B. Radusies situācija, kas attēlota 26.zīmējumā: visi tālākie sējumi līdz rindas galam atrodas vienu vietu pa labi no savas īstās vietas (patiesībā \(A\) gadījums ir \(B\) gadījuma speciālgadījums):

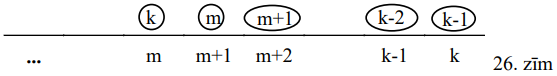
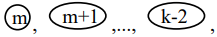
Tad mainām \(k\)-to sējumu tālāk līdz galam. Rezultātā sējumi 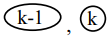nonāk savās vietās rindas labajā galā, bet pirmie \(m-1\) sējumi joprojām nav savās vietās. Atkal varam izmantot induktīvo hipotēzi.

C. Radusies situācija, kad \(t\) sējumi, kas ir pa labi no \(k\)-tā sējuma pašreizējās pozīcijas, atrodas vienu vietu pa labi no savas īstās vietas, bet \((t+1)\)-ais sējums - nē (27.zīm.):

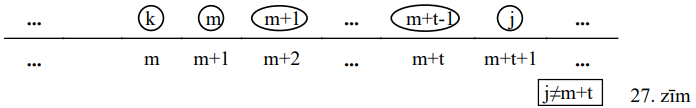
Skaidrs, ka \(j \neq m+t;\ m+t-1;\ m+t-2;\ \ldots;\ m+1;\ m\). Tāpēc varam sējumu 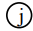"nosūtīt" pa kreisi, kamēr tas samainās ar . Rezultātā neviens sējums nav no jauna nonācis īstajā vietā, bet pabīdījies vienu vietu pa labi. Līdzīgi turpinām, kamēr iestājas \(A\) vai \(B\) gadījums. Induktīvā pāreja izdarīta.