Atrisinājums

Attēlosim kluba biedrus ar kuba virsotnēm. Izvēlēsimies šādas \(4\) virsotņu kopas:

(A) visas \(6\) skaldnes,

(B) visus \(6\) diagonālšķēlumus,

(C) divu kubā "ievilkto" regulāro tetraedru virsotņu kopas (skat. 12.zīm.).

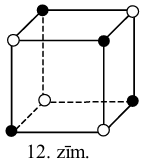
Skaidrs, ka nekādas divas no šīm kopām "nešķeļas" pa triju virsotņu sistēmu. Tātad visi virsotņu trijnieki, kurus tās satur, ir dažādi. Kopā tās satur \(14 \cdot C^{3}_{4}=14 \cdot 4=56\) trijniekus. Tā kā trijnieku pavisam arī ir \(C_{8}^{3}=\frac{8 \cdot 7 \cdot 6}{1 \cdot 2 \cdot 3}=56\), risinājuma pareizība pamatota.