LV.AMO.2019.12.3
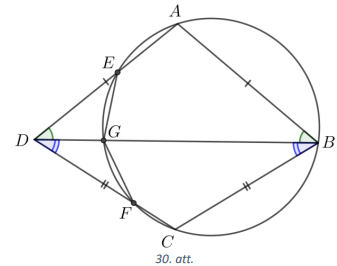
Dots četrstūris \(ABCD\), kuram \(AB=AD\) un \(BC=CD\). Riņķa līnija, kas iet caur punktiem \(A, B\) un \(C\), krusto nogriežņus \(AD\) un \(CD\) attiecīgi to iekšējos punktos \(E\) un \(F\) un nogriezni \(BD\) punktā \(G\). Pierādīt, ka \(EG=FG\).
Atrisinājums
Tā kā \(AB=AD\) un \(BC=CD\), tad trijstūri \(DAB\) un \(DCB\) ir vienādsānu trijstūri un \(\sphericalangle ADB=\sphericalangle ABD=\alpha\) un \(\sphericalangle BDC=\sphericalangle DBC=\beta\) kā leņķi pie pamata (skat. 30.att.). Punkti \(G, E, A, B\) atrodas uz vienas riņķa līnijas, tāpēc \(\sphericalangle ABG+\sphericalangle GEA=180^{\circ}\) jeb \(\sphericalangle GEA=180^{\circ}-\alpha\). No blakusleņķu īpašības iegūstam, ka \(\sphericalangle DEG=180^{\circ}-\sphericalangle GEA=180^{\circ}-\left(180^{\circ}-\alpha\right)=\alpha\). Tātad trijstūris \(DGE\) ir vienādsānu un \(DG=EG\) kā malas pret vienādiem leņķiem.
Punkti \(G, F, C, B\) atrodas uz vienas riņķa līnijas, tāpēc \(\sphericalangle CBG+\sphericalangle GFC=180^{\circ}\) jeb \(\sphericalangle GFC=180^{\circ}-\beta\). No blakusleņķu īpašības iegūstam, ka \(\sphericalangle DFG=180^{\circ}-\sphericalangle GFC=\beta\). Tātad trijstūris \(DGF\) ir vienādsānu un \(DG=FG\) kā malas pret vienādiem leņķiem. Līdz ar to esam pierādījuši, ka \(EG=DG=FG\).