LV.AMO.2019.11.3
Uz trijstūra \(ABC\) malām \(AB\) un \(BC\) izvēlēti attiecīgi tādi punkti \(D\) un \(E\), ka \(AC \parallel DE\). Nogriežņi \(AE\) un \(CD\) krustojas punktā \(F\). Punkti \(B, D, E\) un \(F\) atrodas uz vienas riņķa līnijas. Taisne \(BF\) krusto malu \(AC\) punktā \(H\) un trijstūrim \(ABC\) apvilkto riņķa līniju punktā \(G\). Pierādīt, ka \(FH=GH\).
Atrisinājums
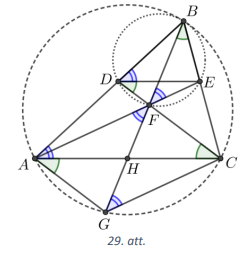
Tā kā četrstūri \(BAGC\) un \(BDFE\) ir ievilkti, tad \(\sphericalangle GAC=\sphericalangle GBC\) un \(\sphericalangle GBC=\sphericalangle FBE=\sphericalangle FDE\) kā ievilktie leņķi, kas balstās uz viena un tā paša loka attiecīgi \(GC\) un \(FE\) (skat. 29.att.). Pēc dotā \(AC \parallel DE\), tad \(\sphericalangle FDE=\sphericalangle FCA\) kā iekšējie škērsleņķi pie paralēlām taisnēm. Līdz ar to \(\sphericalangle GAC=\sphericalangle FCA\), no kā izriet, ka \(AG \parallel\) \(FC\), jo iekšējie šķērsleņķi, ir vienādi.
Arī \(\sphericalangle BAC=\sphericalangle BGC\) un \(\sphericalangle BDE=\sphericalangle BFE\) kā ievilktie leņķi, kas balstās uz viena un tā paša loka attiecīgi \(BC\) un \(BE\). Pēc dotā \(AC \parallel DE\), tad \(\sphericalangle CAB=\sphericalangle EDB\) kā kāpšļu leņķi pie paralēlām taisnēm. Ievērojot, ka \(\sphericalangle AFG=\sphericalangle BFE\) kā krustleņķi, iegūstam \(\sphericalangle GAC=\sphericalangle FCA\). Tātad \(CG \parallel FA\), jo iekšējie škērsleņķi, ir vienādi.
Tāpēc četrstūris \(AFCG\) ir paralelograms, jo tā pretējās malas ir pa pāriem paralēlas. Paralelograma diagonāles krustpunktā dalās uz pusēm, tāpēc \(FH=GH\).