Atrisinājums

(A) jā, skat., piem, 5.zīm.

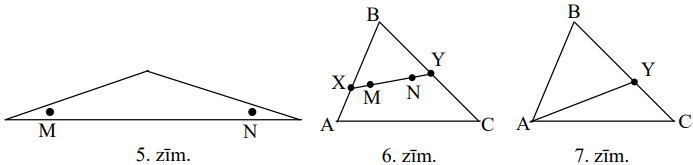
(B) nē. Novelkam taisni \(MN\); pieņemsim, ka tā krusto trijstūra kontūru punktos \(X\) un \(Y\) (6.zīm.) Vispirms pieņemam, ka ne \(X\), ne \(Y\) nav \(T\) virsotne. Tā kā \(\sphericalangle YXA+\sphericalangle YXB=180^{\circ}\), tad viens no šiem leņķiem nav šaurs; varam pieņemt, ka \(\sphericalangle AXY \geq 90^{\circ}\). Tad \(\sphericalangle AXY\) ir lielākais leņķis trijstūrī \(AXY\), tāpēc \(AY\) ir tur garākā mala; tāpēc \(AY>XY>MN\). Tā kā \(\sphericalangle AYB+\sphericalangle AYC=180^{\circ}\), tad viens no šiem leņķiem nav šaurs; ja tas ir, piemēram, \(\sphericalangle AYC\), tad kā iepriekš iegūstam, ka \(AC>AY>XY>MN\). Ja kāds no punktiem ir \(T\) virsotne, uzreiz nonākam pie augšminētā sprieduma otrās daļas.

Piezīme: vērtējumā būs ļoti būtiski, cik pilnīgi skolēna izklāsts aptver visas situācijas.