Atrisinājums

(A) jā; skat.zīm. \(\alpha\)

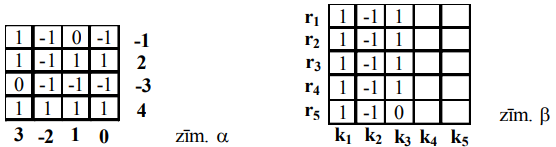
(B) nē. Desmit summām iespējamas vērtības \(0, \mp 1, \mp 2, \mp 3, \mp 4, \mp 5\) (kopā \(11\)). Ja rindiņu summas ir \(r_{1},\ \ldots,\ r_{5}\) un kolonu summas ir \(k_{1},\ \ldots,\ k_{5}\), tad \(\left(r_{1}+\ldots+r_{5}\right)+\left(k_{1}+\ldots+k_{5}\right)\) ir pāra skaitlis. Tāpēc starp \(r_{1},\ \ldots,\ r_{5},\ k_{1},\ \ldots,\ k_{5}\) ir pāra skaits nepāra skaitļu. Tāpēc visas nepāra summas \(\mp 1, \mp 3, \mp 5\) ir sastopamas. Varam pieņemt, ka \(k_{1}=5\). Tad nevar būt \(r_{i}=-5\); tāpēc varam uzskatīt, ka \(k_{2}=-5\) (ievērojam, ka kolonas savā starpā un rindas savā starpā var patvaļīgi mainīt). No summām " \(4\) " un, " \(4\) " vismaz vienai ir jābūt; varam pieņemt, ka ir summa \(4\) (zīmes visiem skaitļiem tabulā var mainīt uz pretējām). Varam pieņemt, ka \(k_{3}=4\) un vienīgā nulle ir rindā \(r_{5}\) (zīm. \(\beta\)). Nevar būt \(r_{i}=-3\); tāpēc kādā kolonā summa ir " \(-3\) ", un uzskatīsim, ka \(k_{4}=-3\). Tātad \(4.\) kolonā ir vismaz trīs " \(-1\) ".

I Tie visi sastopami pirmajās \(4\) rindās; tad varam uzskatīt, ka tie ir pirmajās \(3\) rindās (zīm. \(\gamma\)). Tad pirmajās \(3\) rindās summām jābūt \(-1;\ 0;\ 1\). Tāpēc \(5.\) kolonā pirmajās \(3\) rindās ir skaitļi \(-1;\ 0;\ 1\), un \(k_{5} \neq 3\). Arī \(r_{5} \neq 3\). Vērtība \(3\) var būt tikai \(r_{4}\), tāpēc \(4.\) rindā abi pēdējie skaitļi ir \(1\). Tā kā \(k_{4}=-3\), tad \(4.\) kolonas un \(5.\) rindas krustpunktā ir " \(-1\) ". Lai kā izvēlētos skaitli \(x\), iegūst pretrunu (tieša pārbaude).

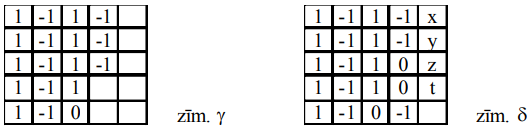
II Ceturtajā kolonā pirmajās \(4\) rindās ir tikai divi " \(-1\) ". Varam uzskatīt, ka situāciju attēlo zīm. \(\delta\). Nevienā rindā summa nevar būt \(3\), tāpēc \(k_{5}=3\). Tas iespējams vai nu kā \(1+1+1+0+0\), vai kā \(1+1+1+1+(-1)\). Jābūt \(x \neq y\) un \(z \neq t\). Pārbaudot visas iespējas, katrā no tām iegūst pretrunu.